Teaching for Mastery

‘Teaching for mastery’ is a much-used phrase, yet there is often misunderstanding of what it refers to. Before outlining what is meant by teaching for mastery, it is worth considering the intended outcome, which is for pupils to achieve mastery of the mathematics in the curriculum.

When a pupil has mastered something in mathematics, it is useful to think of what we might see or hear them being able to do and the bullet point list below provides a useful framework. When a pupil has mastered something in mathematics, they can:

• describe it in their own words;
• represent it in a variety of ways (using manipulatives, drawings and symbols);
• explain it to someone else;
• make up their own examples (and non-examples) of it;
• spot connections between it and other ideas;
• recognise it in new and unfamiliar problems or contexts;
• make use of it in new or unfamiliar situations.

In order to achieve this, we need to actively teach for mastery. Teaching for mastery involves considering our own beliefs and knowledge of mathematics, and also how we can teach it most effectively.

A teaching for mastery approach is founded on the belief that virtually all pupils are capable of being successful in mathematics and that, to develop mastery takes good teaching and intelligent practice, rather than any particular natural gift. Related to this is the belief that mathematics is a problem-solving activity that involves developing deep conceptual understanding as well as procedural knowledge, and this leads to the ability to solve complex and unfamiliar problems.

In order to live this out day-to-day in the classroom, teachers need to develop their mathematical subject knowledge for teaching and understanding of effective pedagogy. Much of our work is founded upon developing knowledge and understanding of the ‘Five Big Ideas’ which have been developed by the NCETM. These pedagogical principles are a synthesis of research and literature from around the world into effective mathematics teaching. Below is a commonly used diagram to show these ideas with some supporting explanation of each one.

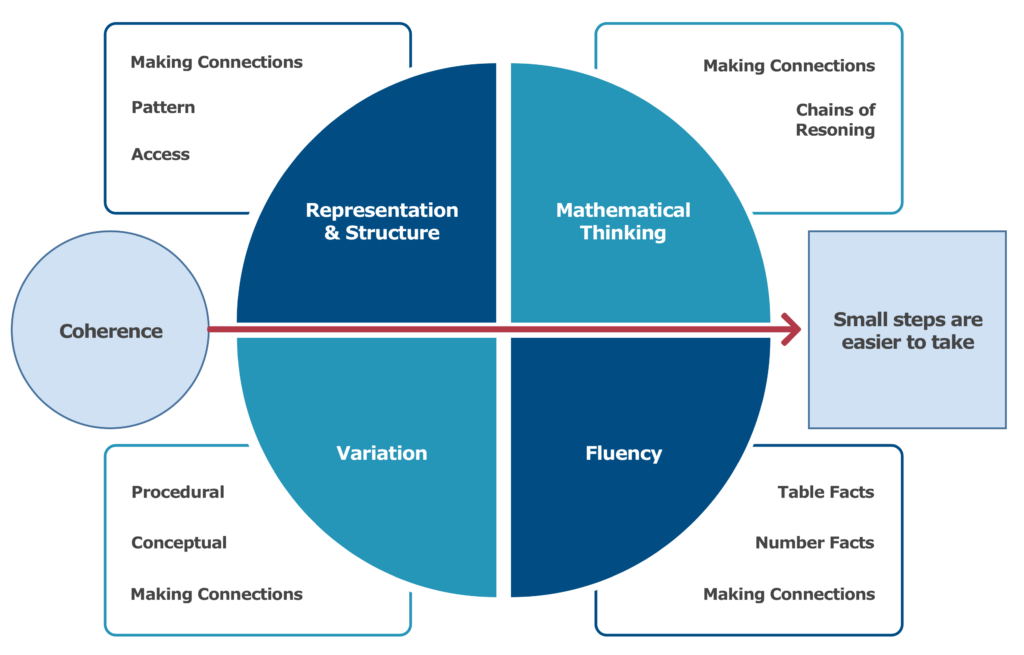
Representation and Structure
Representations used in lessons expose the mathematical structure being taught, the aim being that students develop a deep and multi-dimensional understanding of the mathematics being taught. An important skill to develop is to ‘translate’ between representations, and pupils should not be dependent on any one representation.

Mathematical Thinking
If taught ideas are to be understood deeply, they must not merely be passively received but must be worked on by the student – thought about, reasoned with and discussed with others.

Fluency
Fluency in mathematics involves three main aspects: efficiency, accuracy and flexibility. Efficiency refers to using a combination of known facts and mental methods to calculate fluently. Accuracy means just that – being accurate in the process of recording and checking. Flexibility refers to pupils having a ‘toolkit’ of strategies that they can choose from rather than being tied to any one particular method.

Variation
Variation is twofold. It is firstly about how the teacher represents the concept being taught, often in more than one way, to draw attention to critical aspects, and to develop deep and holistic understanding. It is also about the sequencing of the episodes, activities and exercises used within a lesson and follow up practice, paying attention to what is kept the same and what changes, to connect the mathematics and draw attention to mathematical relationships and structure.

Coherence
None of the above four things are likely to have significant impact unless they are brought together in a coherent way. Lessons should be broken down into small connected steps that gradually unfold the concept, providing access for all children and leading to a generalisation of the concept and the ability to apply the concept to a range of contexts.